Quantum Geometry

Wave Functions

MIT physicists and colleagues measured the geometry, or shape, of electrons in solids at the quantum level. Scientists have long known how to measure the energies and velocities of electrons in crystalline materials, but until now, those systems’ quantum geometry could only be inferred theoretically, or sometimes not at all.

Momentum Space

Prof. .Nat Abdel Nasser Tawfik

Our quantum geometric approach is demonstrated through a graphical representation of geometries, describing the replacement of one geometry with another. Max Born's proposal to substitute the classical four-dimensional Riemann geometry with a four-dimensional momentum space geometry did not lead to the quantization of general relativity due to the absence of a mechanism for the curvature of momentum space at that time. It was only four decades ago that the concept of non-commutative relations was believed to offer a solution for the curvature of momentum space. Caianiello introduced an eight-dimensional space consisting of classical spacetime and additional four-dimensional tangents, while Brandt demonstrated that the extra dimensions could represent momentum space without relying on Finsler geometry. Recently, efforts have been made to rigorously introduce Finsler geometry, considering its mathematical properties, to complete this task. The graphical representation of this journey throughout the last century is depicted in the first image.

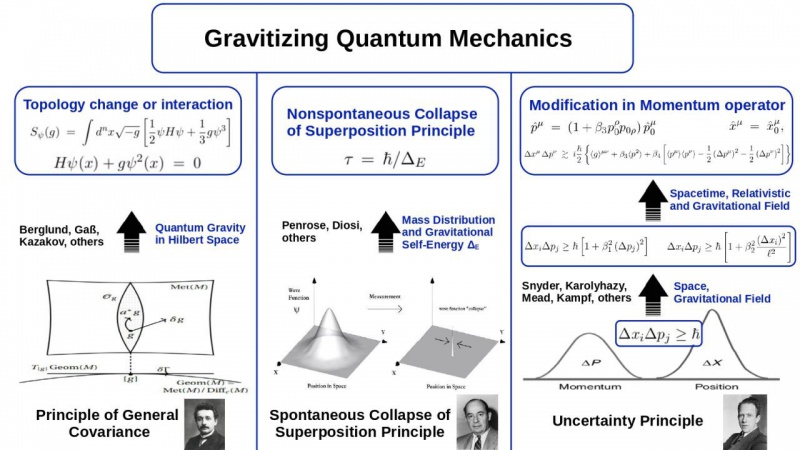
Our proposed unification approach of the two fundamental theories (relativity and quantum) goes beyond simply extending the geometries of general relativity. As important as geometry, we also introduce necessary modifications to quantum mechanics in order to incorporate gravitational effects. The second picture illustrates three different methods for generalizing quantum mechanics by including gravity. One of these methods focuses on Heisenberg's uncertainty principle, while the second method addresses the collapse of quantum superposition principle, for which von Neumann suggested "measurement" as the key mechanism. The third method introduces dynamics through general covariance, a concept originally introduced by Einstein in the context of general relativity. All of these approaches aim to integrate gravitational fields, or relativistic gravitational fields, into quantum mechanics. This is achieved by modifying quantum mechanics through the generalization of the Schrödinger equation. Our chosen method involves modifying the momentum operator based on the uncertainty principle. A comparison of the two pictures reveals how the integration of the two generalizations (that is quantum mechanics and that of geometry) will take place. Specifically, the modification of the momentum operator depicted in the second picture will be integrated into the geometry of the eight-dimensional cotangent space, particularly the portion related to momentum.

Quantum Geometric Tensor

Understanding the geometric properties of quantum states and their implications in fundamental physical phenomena is a core aspect of contemporary physics. The quantum geometric tensor (QGT) is a central physical object in this regard, encoding complete information about the geometry of the quantum state. The imaginary part of the QGT is the well-known Berry curvature, which plays an integral role in the topological magnetoelectric and optoelectronic phenomena. The real part of the QGT is the quantum metric, whose importance has come to prominence recently, giving rise to a new set of quantum geometric phenomena such as anomalous Landau levels, flat band superfluidity, excitonic Lamb shifts and nonlinear Hall effect. Despite the central importance of the QGT, its experimental measurements have been restricted only to artificial two-level systems. Here, we develop a framework to measure the QGT in crystalline solids using polarization-, spin- and angle-resolved photoemission spectroscopy. Using this framework, we demonstrate the effective reconstruction of the QGT in the kagome metal CoSn, which hosts topological flat bands. Establishing this momentum- and energy-resolved spectroscopic probe of the QGT is poised to significantly advance our understanding of quantum geometric responses in a wide range of crystalline systems.